二进制数中1的个数
naive,一位一位数
1
2
3
4
5
6
7
8
9
10
11unsigned int popcount(unsigned int x) {
unsigned n = 0;
for (int i = 0; i < 32; i++) {
if (x == 0) {
break;
}
n += x & 1;
x = x >> 1;
}
return n;
}相对暴力,只数有1的位,复杂度O(有多少个1)
1
2
3
4
5
6
7
8unsigned int popcount(unsigned int x) {
unsigned n = 0;
while (x) {
x = x & (x - 1);
++n;
}
return n;
}二分法, 复杂度O(log32)
1
2
3
4
5
6
7
8
9
10
11unsigned int popcount(unsigned int n) {
/*
* swar algorithm, work on 32 bit integer
*/
n = (n & 0x55555555) + ((n >> 1) & 0x55555555);
n = (n & 0x33333333) + ((n >> 2) & 0x33333333);
n = (n & 0x0F0F0F0F) + ((n >> 4) & 0x0F0F0F0F);
n = (n & 0x00FF00FF) + ((n >> 8) & 0x00FF00FF);
n = (n & 0x0000FFFF) + ((n >> 16) & 0x0000FFFF);
return n;
}想法类似二分,两两相加
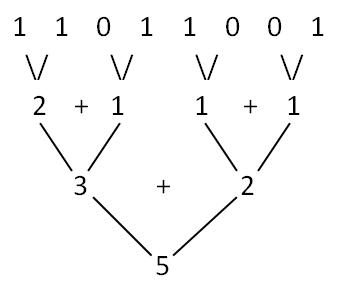
将32位数看成相互独立的32个 0-1 数字,
然后两两相加, 这样我们就有16个数字了,
然后再两两相加, 就变成8个数字了,
接着再两两相加变成4个,
然后两个, 最后一个数字,
由于是32位数字的和, 所以答案刚好就是1的个数啦。1
2
3
4
5右移 1位. 与数字: 01010101010101010101010101010101 => 0x55555555
右移 2位. 与数字: 00110011001100110011001100110011 => 0x33333333
右移 4位. 与数字: 00001111000011110000111100001111 => 0x0F0F0F0F
右移 8位. 与数字: 00000000111111110000000011111111 => 0x00FF00FF
右移16位. 与数字: 00000000000000001111111111111111 => 0x0000FFFF查表,预先算好,查询时直接读
表的大小可以改,比如256,适当取
1
2
3
4
5
6
7
8
9
10
11
int table[MAXN];
void pre() {
for (int i = 1; i < MAXN; i++) {
table[i] = table[i >> 1] + (i & 1);
}
}
unsigned popcount(unsigned x) {
return (table[x >> 16] + table[x & 0xFFFF]);
}